Least Squares Regression and Residual Plots (Topic 2.7)
Chapter 3 - Day 5
Unit 2
Chapter 3
Day 1
Day 2
Day 3
Day 4
Day 5
Day 6
Day 7
Day 8
Day 9
Day 10
Day 11
Day 12
Day 13
Day 14
All Units
Learning Targets
-
Determine the equation of a least-squares regression line using technology or computer output.
-
Construct and interpret residual plots to assess whether a regression model is appropriate.
Activity: How many iPhones will be sold?
Before you begin the activity, it's worth discussing with your students, "How does the computer or calculator find the line of “best” fit? What makes it the line of best fit?" Using this Desmos eTool we let students try to move the line into the “best” spot (be sure you hide the line of best fit to start). They discovered that the the line of “best” fit is the one that minimizes the sum of the squared residuals (the least squares regression line!). This can also be done nicely using the statistical software Fathom. Now students are ready for the activity!
The iPhone 8 was just announced, and we were wondering how many Apple will sell. To help us make a good prediction, we looked up the sales for all the previous iPhones. Apple stopped releasing sales data after the iPhone 6S. It turns out that this data set is a beautiful example of nonlinear data. Even so, students are asked find a line of best fit, and then examine the residuals. In the end, we want students to understand how to make a residual plot and to recognize that a pattern in the residual plot is a signal that the model we have chosen is not appropriate.
Teaching Tip:
When asked if a linear model is appropriate, students will sometimes incorrectly use only the correlation value, r, to justify linearity. However, a strong correlation value doesn’t mean an association is linear. An association can be clearly nonlinear and still have a correlation close to ±1. Only a residual plot can adequately address whether a line is an appropriate model for the data by showing the pattern of deviations from the line. For example, graphing the function y = x^2 for the integers 1 to 10 yields a correlation of r = 0.97, but the residual plot shows an obvious pattern.
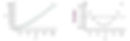
Should I have students make residual plots on the calculator?
Luke's Lesson Notes
Here is a brief video highlighting some key information to help you prepare to teach this lesson.


